A Brief Look at Zone of Proximal Development

Lev Vygotsky (1896 -1934) was a pioneer psychologist who lived in Moscow. I have great respect for his studies and found his Mind And Society an absorbing read. One of the precious ideas he brought to us is what he called the Zone Of Proximal Development. I was reminded of this recently when reading Laurie Bartel’s post, Lev Vygotsky & ZPD, where she called for elaboration or clarification of ZPD.

Vygotsky had an interest in scaffolding, particularly in relation to learner development in vocabulary and language. He was fascinated with ways of determining the state of development in the young learner. He drew the distinction between what he referred to as ‘age level of development’ and the ‘developmental process’ in relation to ‘learning capabilities’.

Closer analysis

Vygotsky’s studies in this field suggest he firmly believed there was more to potential development in the learner than just what could be judged by observing what he called the learner’s actual development level. This is what can be determined presumably through analysis over a range of tests and other related observational parameters.

His argument was that what the young learner can do with the assistance of others is a better indicator of mental development than what she can do alone. He made the unambiguous distinction between the assessable accomplishment of the learner when unaided and the observable performance of the learner when given assistance. His pithy summary is

The zone of proximal development defines those functions that have not yet matured but are in the process of maturation, functions that will mature tomorrow but are currently in an embryonic state.

Much of Vygotsky’s ideas were tempered by existing theory of the time and furthered by his insightful hypotheses based on his own observations. R G Tharp and R Gallimore proposed an expansion of Vygotsky’s zone of proximal development that involved further stages including the assistance that could be provided by the learner herself.

While Vygotsky spoke of developmental stages in the learner, he also posited that development is too complex to be defined by stages that disperse and become diffuse as the learner develops. As a result of this diffusion, previously identifiable stages can no longer be recognised in the learner.


Rather than ‘development’ laying down a series of identifiable zones, as shown above, learning is more a broad frontier that advances progressively. The zone of proximal development at the periphery of the actual development level has a depth according to the level of potential development.


“What is in the zone of proximal development today will be the actual developmental level tomorrow”.

Learning, Models and Other Tricks

courtesy Wordle

Have you ever thought why models are so often used in teaching and learning? They formed part of what used to be called teaching aids, more recently termed learning resources.

In the high school that I attended, we had a resource room. Senior students were given access to this room for study purposes and when helping a teacher prepare lessons. The day I was permitted into the resource room I could not stop thinking about the amazing things I saw stored there. It was only years later when I became a teacher that I realised why my teachers had guarded the room and its content so vigilantly and with such reverence.

Effecting learning

I recently ran my blog through Wordle. The result at the head of this post shows what has obviously been the most important thing on my mind when I wrote recent posts. It also made me think that despite my familiarity with the word, learning and how it is brought about is not always looked upon as common ground when discussed in depth with others in the field. Tony Karrer’s recent post has hosted a debate on ways of learning and associated ideas, a follow up to his post on Learning Goals.

Learning by association

The renowned scientist, Dr Jacob Bronowski, who was also an intellectual, expert code-cracker, mathematician and author, gave celebrated lectures on BBC TV in the 1960s. During one of his lectures, he demonstrated how a feat of memory through association could be performed, and he displayed this both by his own memory acumen and with the help of a trained member of his audience.

The 'trick' involves some preparation. A list of (say) 20 commonly known items, personal to the memoriser, is committed thoroughly to memory so that not only the list order can be recalled but also the position in that list of any of its component items.

Once this is accomplished, the memoriser is then shown a series of up to 20 new items in sequence, such as cards drawn randomly from a full pack of playing cards. For each new item shown, the memoriser simply ticks it in the mind by association with each of the previously memorised personal items in sequence.

When complete, the memoriser is asked to name an item by its number in the list and knows what the item is. As splendidly amazing as this act appears when first seen, it is based on learning by association. While it is true that this method has limited application to some learning, it shows how rapid and facile the mind and memory can be in the simple act of learning content.

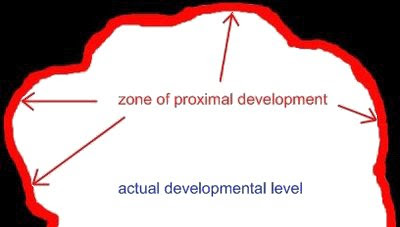
Models and their place in learning

Learning by association is not a new idea. It is the working part of how learning is assisted when a model is used. It is called upon when a map is used in learning geography or an elaborate digital model is used in learning the function of interior parts of a plant cell. Models work by drawing on previous experiences and learnt ideas, and relating to these when learning something new.

Often the simplest models are the best, even when they may relate to a complicated theory, concept or phenomenon. Though elaborate models may look fascinating, they rarely convey useful learning to the beginner. Learners need to be already familiar with parts of the model itself. As intricate and captivating as the Watson, Crick and Wilkins model of DNA may be, it conveys nothing about its chemistry to those who have never learnt elementary Chemistry.

courtesy NASA

Learning and memory

It is well known that before any skill can be acquired learning a second language, knowledge of vocabulary is fundamental. It is also becoming recognised by educators that the language of a subject, and knowledge of vocabulary in particular, is required for the learner to be able to think in terms of the subject and also to converse about it with others.

Without the vocabulary of a hitherto unknown subject it is impossible for a beginner to acquire any useful subject skill. Motor skills have similar fundamental elements when it comes to the first time learner picking up the ropes of a new skill.

There is no evidence to suggest that the memory required while learning and remembering a vocabulary (content learnt by association) is fundamentally different from that needed to learn and remember the higher skills. When concepts or skills to be learnt become more complicated as the learner progresses, a stage is invariably reached where the learner has to work at them to make the leaps. Once made, these too can be learnt and remembered. Higher thinking skills are required to be learnt to continue to progress. This is often forgotten by the expert who is addressing learning in the subject, the so-called cognitive apprenticeship theory.

Learning is recursively elaborate

A concept, idea or formula learnt in one discipline can find a use in another that’s seemingly unrelated. A child who recognises the relationship between similar patterns of learning in two distinct disciplines makes a cognitive leap. Intelligence is intimately linked with the ability to connect patterns in this way.

The animated equations depicted here are of elementary algebra. They show how the same basic tactic can apply to two distinct areas of learning in Science. A child who masters the simple algebra relevant to this also learns the skill to work within an unbelievably large number of its applications. The scope for it is huge, and it finds use in many common everyday tasks, from a simple calculation in an expenses return to estimating how long a car journey is likely to take.

This recursive application of algebra is by no means a unique feature in learning, for there are many millions of patterns that cross seemingly unrelated disciplines. The ability to understand and recognise these patterns is one that is familiar to the compilers of intelligence tests. It was believed that such tests, according to various scales, could be used to classify and measure cognitive ability. Though there may well be some merit in the idea of pattern recognition being linked to cognitive ability, the means created to measure this fell short of something useful, never mind fairness.

Cutting corners

The recursive nature of learning often compels us to take short cuts that sometimes lead to a misunderstanding that a concept has been learnt. It may even suggest that it doesn’t need to be learnt; the word content springs to mind. I’ll use an example from elementary Chemistry to demonstrate this.

Finding the chemical formula for a simple compound, such as aluminium oxide, can be done a number of ways, all of which have the potential to yield the same answer:

1. use Google - provided the student can apply the search routine and recognises a reputable site when one is brought up, the correct formula might be found,
   
   
2. recall the chemical symbols for the elements oxygen and aluminium, and that oxygen has a valency of 2 and aluminium has a valency of 3, then apply the recalled rule for writing correct chemical formulae,
   
   
3. referring to the periodic table of the elements (or just simply knowing it) the student uses the atomic number of oxygen to write the electron configuration of its atom - having used a similar process to write the electron configuration of aluminium, the student may determine the common valencies of both elements and then apply method 2.
   

Understanding how the formula is found is part and parcel of understanding so-called ‘valency theory’ in Chemistry. Learners who can Google the formula for any simple chemical compound don’t really need to know much chemistry. While method 2 barely touches on some of the principles involved in valency theory, knowledge of how to use method 3 takes the learner closer towards how to apply that theory and to understanding why chemical compounds form between elements in the first place.

Most students who go on to study Chemistry in senior school will learn both methods 2 and 3. They may become so proficient at writing chemical formula using method 2 that they can write several correct formula in the time it takes another student to type in the Google search criteria in following method 1, let alone what’s needed to choose a suitable trustworthy site to browse.

All of the above methods for finding a formula can be learnt and each method has its merit depending on the need. But to say that all a learner needs to know is how to use an Internet search engine to find the formula of a simple chemical compound is not actually learning any Chemistry. Yet this is often used as an argument for not teaching content. There comes a time when the learner just has to face learning some content, and this applies to many distinct disciplines.

Models can be conflicting

One of the many curious phenomena studied in secondary school Science is that of the behaviour of light. This well studied topic requires a series of models to explain how light can behave in different circumstances. A feature of two celebrated models for light, that of the particle or photon and that of the wave, is that neither model explains all the observable properties of light.

While both these models can be used to explain and predict the behaviour of other phenomena not directly related to light, it takes an enlightened learner to understand that they are just models. This peculiarly useful awareness is a higher learning skill. It allows the learner who is very familiar with models used within a discipline to understand their limitations and permits recognition of when a particular model is applicable and when it is not. Recognising that a model and the phenomenon it mirrors are not the same things is extremely important in Science.

The lesser analogy

Unlike the model, an analogy is not trying to depict in any way how the thing or concept exists. It is a direct mapping between unrelated elements of one idea and another. There is no need for there to be any true resemblance between the thing or concept and its parallel used in analogy.

Unfortunately, analogies are often used erroneously as models. For the learner, the analogy is far more involved, the behaviour of one thing being considered while thinking of the associated behaviour of another.

It calls for the most use of imagination, being a parallelism that’s left mainly up to the ingenuity of the thinker. As they are necessarily specific, analogies are severely limited in their broader application.

Facile in association

The mind seems to be facile in the way it can link seemingly unrelated things and learn by association. Perhaps this is why the model enjoys its time honoured place in learning at all levels, for it is so successful.

Models enable a direct mapping of what is seen onto what is being learnt. Good models permit this to be assimilated easily by the learner so that they can apply what’s learnt. Through pattern recognition learners can find further application of what they have learnt.

The enlightened learner, who also understands the difference between the model and the idea, concept or phenomenon that it is mirroring, can flip between models used to reflect these. Introducing the learner to this important difference between the model and what it reflects is the province of good teaching.

In Defense of Occam’s (Ockham’s) Razor

There’s been a lot said about Occam’s Razor on the Net recently, though not always supportive of its application. Also known as the law of economy, or the law of parsimony, it derived its name from a principle held by the medieval scholar William of Ockham.

He is believed to have said non sunt multiplicanda entia praeter necessitatem - entities are not to be multiplied beyond necessity. It is thought that this principle may have been broached before Ockham by a French Dominican theologian Durand de Saint-Pourcain (1270 - 1334).

A well used blade

It has been used in many disciplines. Science in particular has enjoyed its application over the centuries and it has been exploited a fair bit in philosophy – Nicole d’Oresme, Galileo, Newton and Einstein all drew on Occam’s Razor in some form in their studies. Einstein used it in his theory of special relativity that predicted that the lengths of objects shorten and watches slow down when they move. In considering the tangible, explicit aspects of a theory, Stephen Hawking, in A Brief History of Time, claims “it seems better to employ the principle known as Occam's razor and cut out all the features of the theory that cannot be observed.”

Stroppy criticism

Lately the principle seems to have come under the knife, and it’s validity as a tool has recently been given the chop by several writers.

Is it condemned to the scrap-heap of pre-21st century gadgets?

Or is there life in the old blade yet?

These questions came to mind when I read Peter Turney’s post, Ockham’s Razor is Dull. He speaks disparagingly of its use in the theoretical context of machine-learning and cites Geoffrey Webb’s “Further Experimental Evidence against the Utility of Occam's Razor”. Webb criticises Occam’s Razor for it is found that it doesn’t always work when commonly applied to modern machine-learning.

While I’ve no doubt that Turney’s opinion has some merit, I feel that the original intention behind the principle of Occam’s Razor has been forgotten, or at least severely misunderstood in its application to machine-learning. I suspect the initial application of the principle in such a context was ill-advised, that it was assumed as a means to an end rather than a way of viewing things.

A useful cutter

Occam’s Razor is often applied in many acute and incisive ways. Approximations when quoting populations, expressed to the nearest thousand heads, have been shaved by it. The so-called rounding up of numbers involves its use in trimming away minor fractional odds and ends. But its willy-nilly application can cause sharp problems for the unwary, as any keen statistician or accountant can attest.

It is most fittingly used as a way of looking at abstractions. For some practical purposes it can be brought into play when a decision is to be made on what to select as best from an array of ideas, or processes and strategies that give rise to almost identical outcomes.

Phil Gibb’s useful statement of the principle for scientists is "when you have two competing theories which make exactly the same predictions, the one that is simpler is the better." In that regard it has application in efficient decision making.

It’s all to do with what is perceived to be significant. I suspect that the ability to discern keenly is a vital component of the capacity to use the device effectively. This talent, present almost subconsciously in some people, may be what puts human sensitivity to differentiate well, above that of a machine.

Gibbs’ delightfully brief “What is Occam’s Razor?” lists an array of statements that seem to have been derived from the principle:

If you have two theories which both explain the observed facts then you should use the simplest until more evidence comes along.

The simplest explanation for some phenomenon is more likely to be accurate than more complicated explanations.

If you have two equally likely solutions to a problem, pick the simplest.

The explanation requiring the fewest assumptions is most likely to be correct.

Keep it simple, otherwise known as the KIS approach.

A worthwhile tool

It is an excellent tool to apply when looking for a model or a metaphor to use in a learning context. Map makers use its principle when simplifying the features of a landscape in two dimensions. The famous colourful London Underground Tube maps, aside being now considered works of art, are splendid examples of the practical use of Occam’s Razor as a design tool.

Current concerns expressed by many bloggers about the glut of data, otherwise known as infowhelm, could well be emeliorated by the judicious and skillful wielding of the blade. A honing of the discerning abilities may help to carve away redundant or duplicated information. Methods for trimming and blood-letting the burgeoning plethora of knowledge on the Internet are ripe for reaping.

Simplification is its keenest feature. A slice or so could well put Occam’s Razor at the cutting-edge of 21^st century knowledge management.